Question

A 39-cm-long vertical spring has one end fixed on the floor. Placing a 2.2 kg physics textbook on the spring compresses it to a length of 29 cm.What is the spring constant?

Answer 1

To solve this problem we will apply Hooke's law. Which says that the force on a spring is equivalent to the product between the elastic constant and the displacement of the spring.

`F = k x`

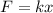
Here,

k = Spring constant

x = Displacement

Rearranging to find the spring constant,

`k = (F)/(x)`

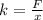
Spring compresses it to 29 cm so

`x = 39- 29 = 10 cm`

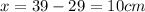
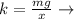`k = (mg)/(x) \rightarrow` The force in this case is equivalent to the weight of the spring

`k = \frac{2.2 * 9.8}{10 * 10 ^ {-2}}`

`k = 215.6N/m`

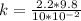
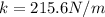
Therefore the spring constant is 215.6N/m