Answer:
(a) 01 + 1011
Convert the two numbers into their 4-bit representation.
=> 01 = 0001
=> 1011
Addition of the two numbers (in their 2's complement form) gives the following:
0 0 0 1 ------------------> + 1 (in decimal)
1 0 1 1 ------------------> - 5 (in decimal)
1 1 0 0 -------------------> - 4 (in decimal)
Explanation for (a)
01 or 0001
Since the most significant bit is 0 (leftmost bit), it shows that it is a positive number. Therefore, it can be directly converted to its decimal representation as follows:
0001 = 0 x
 + 0 x
+ 0 x
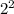 + 0 x
+ 0 x
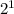 + 1 x
+ 1 x
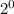 = 1
= 1
0001 is + 1 in decimal.
1011
Its most significant bit(MSB) is 1 showing that it is negative.
Flipping all its bits and adding 1 to the result, will convert it to it's positive counterpart.
i.e 1011 => 0100 + 1 = 0101.
Converting the result (0101) to decimal gives
0101 = 0 x
 + 1 x
+ 1 x
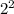 + 0 x
+ 0 x
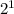 + 1 x
+ 1 x
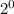 = 5
= 5
1011 is -5 in decimal
01 + 1011 or 0001+ 1011 = 1100
The result (1100), of the addition of the two numbers, is a negative number as the MSB is 1.
Convert it to it's positive counterpart.
i.e 1100 => 0011 + 1 = 0100.
Converting the result (0100) to decimal gives
0100 = 0 x
 + 1 x
+ 1 x
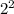 + 0 x
+ 0 x
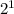 + 0 x
+ 0 x
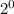 = 4
= 4
Therefore, the result, 1100 is -4 in decimal.
===================================================
(b) 11 + 01010101
Convert the two numbers into their 8-bit representation since one of them is in 8-bit.
PS: Taking 11, its MSB is 1 showing that it is a negative number. Also, it's 8-bit representation will mean pre-padding it with ones(1s) rather than zeros as follows. In other words, pre-padding a 2's complement number is done using its sign bit.
=> 11 = 11111111
=> 01010101
Addition of the two numbers (in their 2's complement form) gives the following:
1 1 1 1 1 1 1 1 ------------------> - 1 (in decimal)
0 1 0 1 0 1 0 1 ------------------> + 85 (in decimal)
1 0 1 0 1 0 1 0 0 -------------------> + 84 (in decimal)
Discard the carry-out bit (1) making the result 01010100
Explanation for (b)
11 or 11111111
Its MSB is 1 showing that it is negative.
Convert it to it's positive counterpart.
11111111 => 00000000 + 1 = 00000001
Converting the result (00000001) to decimal gives 1
11 or 11111111 is - 1 in decimal.
01010101
Its MSB is 0 showing that it is also positive. Now, convert to decimal
01010101 = 85
01010101 is + 85 in decimal.
11111111 + 01010101 = 01010100
The result (01010100), is also positive as the MSB is 0. Now, convert to decimal.
01010100 = 84
Therefore the result (01010100) is + 84 in decimal.
===================================================
(c) 0101 + 110
Convert the two numbers into their 4-bit representations.
=> 0101 = 0101
=> 110 = 1110
Addition of the two numbers (in their 2's complement form) gives the following:
0 1 0 1 ------------------> + 5 (in decimal)
1 1 1 0 -----------------> - 2 (in decimal)
1 0 0 1 1 -------------------> + 3 (in decimal)
Dicard the carry-out bit (leftmost bit) to get 0011 as result.
Explanation for (c)
0101
Since the MSB is 0 (leftmost bit), it shows that it is a positive number. Now, convert to decimal.
0101 = 5
0101 is +5 in decimal.
110 or 1110
Its MSB is 1 showing that it is negative.
Convert it to it's positive counterpart.
i.e 1110 => 0001 + 1 = 0010.
Converting the result (0010) to decimal gives
0010 = 2
1110 is -2 in decimal
0101 + 110 = 0101+ 1110 = 0011
The result (0011), is a positive number as the MSB is 0.
Converting the result (0011) to decimal gives
0011 = 3
Therefore, the result, 0011 is 3 in decimal.
===================================================
(d) 01 + 10
Convert the two numbers into their 4-bit representation.
=> 01 = 0001
=> 10 = 1110
Addition of the two numbers (in their 2's complement form) gives the following:
0 0 0 1 ------------------> + 1 (in decimal)
1 1 1 0 ------------------> - 2 (in decimal)
1 1 1 1 -------------------> - 1 (in decimal)
Explanation for (d)
01 or 0001
Since the MSB is 0 (leftmost bit), it shows that it is a positive number. Now convert to decimal.
0001 = 1
0001 is + 1 in decimal.
1110
Its MSB is 1 showing that it is negative.
Convert it to it's positive counterpart.
i.e 1110 => 0001 + 1 = 0010.
Converting the result (0010) to decimal gives
0010 = 2
1110 is -2 in decimal
01 + 1011 or 0001+ 1110 = 1111
The result (1111), is a negative number as the MSB is 1.
Convert it to it's positive counterpart.
i.e 1111 => 0000 + 1 = 0001.
Converting the result (0001) to decimal gives
0001 = 1
Therefore, the result, 1111 is -1 in decimal.