Answer:

Explanation:
Step 1: First apply radical rule in the given expression.
![\sqrt[n]{a}=a^{(1)/(n)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/9yxc17yxv4j6wrlds6pogdbbsgooqj7u9d.png)
Here,
![\sqrt[3]{7}=7^{(1)/(3)}, \sqrt[5]{7}=7^{(1)/(5)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/kgj3wh92a1v0yjzz82y0ppxe7lw4j1ffgv.png)
The expression becomes
![\frac{\sqrt[3]{7}}{\sqrt[5]{7}}=\frac{7^{(1)/(3)}}{7^{(1)/(5)}}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/uf51v5tbobqbgbf7copmm8b8ogonss0pwx.png)
Step 2: Now, apply exponent rule in the above expression
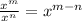
So, the expression becomes,
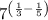 .
.
Step 3: Take cross multiply the denominator and numerator of the fraction in the power of 7.
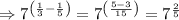
The answer is
 .
.
Hence the simplified form of
![\frac{\sqrt[3]{7}}{\sqrt[5]{7}}=7^{(2)/(5)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/utuaz99bu6yl4hoigpc8dgzbixzog1hjia.png) .
.