Answer:
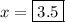
Explanation:
Given:
AC = 5
BC = 6
DB = 4.2
∠ACD ≅ ∠BCD
AD =

∵ ∠ACD ≅ ∠BCD
∴ CD is the angle Bisector of ∠ ACB
We know that, from angle bisector theorem that,
The angle bisector of an interior angle of a triangle divides the opposite side in two segments such that the two segments are proportional to the other two sides of the same triangle.
Therefore, the sides that are in proportion are given as:
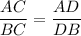
Substituting the given values we get:
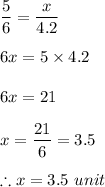
Therefore, the value of
 is 3.5.
is 3.5.