Question

Two steel factories are currently emitting 8,000 tons of pollution each (for a total of 16,000 tons). Pollution reduction (abatement) costs for Plant 1 are given by MCR1= 0.02Q and for Plant 2 by MCR2 = 0.03Q, where Q represents tons of abatement, and MCR the marginal cost of pollution reduction.A. Suppose a regulation is implemented that requires each firm to reduce its pollution by 4,000 tons. What will be each firm’s pollution control costs? Draw two graphs (one for each firm) to support your answer.B. Suppose instead that a pollution tax of $240 per ton of pollution emitted is implemented. How much will each firm now pay in pollution reduction costs (not considering taxes)? How do total pollution reduction costs with the tax compare to the total costs from part (a)? Briefly explain why the costs differ. How much does each firm pay in taxes?

Answer 1

a) attached files.

b) if they are forcer to decrease pollution by 4,000 tons then:

firm A cost 160,000

firm B cost 240,000

c) if there is a ton of $240 per ton oth firm will find more attractive to emliminate pollution than to pay taxes.

Step-by-step explanation:

Marginal cost for Plant 1 = 0.02Q

Marginal cost for Plant 2 = 0.03Q

The marginal cost represent the derivate of the cost fuction

so we solve for the cost function as follow:

`(dF(x))/(dx) x^(a) = a * x^(a-1)`

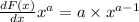
we got 0.02 as dC(q)/dq

so the cost fuction is:

`(dC(q))/(dq) = 2 * 0.01q^(1) \\C(q) = 0.01q^(1+1) = 0.01q^(2)`

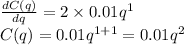
same procedure for hte second plant

`(dC(q))/(dq) = 2 * 0.015q^(1) \\C(q) = 0.015q^(1+1) = 0.015q^(2)`

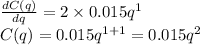
Now we made the graph of this function

We slve for q = 4,000

0.01 x 4,000^2 = 160,000

0.015 x 4,000^2 = 240,000

If there is a tax for 240 dollar per ton then, the factory will eliminate tons up to that amount so it finds equilibrium.

0.02q = 240

q = 240/0.01 = 12,000

Plant 1 will eliminate the entire 8,000 tons as is below the tax floor

Plant 2

0.03q = 240

q = 240/0.03 = 8,000

Plant 2 will also eliminate pollution as is preferable to pay the taxes.