Answer:
Range: {-300, -210, 0, 72}
Explanation:
Given:
Cost price of each camera = $300
The function for profit 'p' is given as:
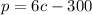
Where, 'p' is the profit and 'c' is the number of cameras sold.
The domain of the function is: {0, 15, 50, 62}
Now, range is the output of the above function for the given domain.
Here, 'c' is the independent variable and hence the domain.
So, plugging in the values of 'c' in the above function will give the set of values of range.
For
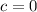 , the profit is given as:
, the profit is given as:
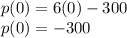
For
 , the profit is given as:
, the profit is given as:
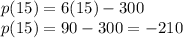
For
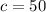 , the profit is given as:
, the profit is given as:
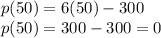
For
 , the profit is given as:
, the profit is given as:
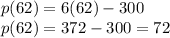
Therefore, the range of the given function is: {-300, -210, 0, 72}
The above range represents the profit of the store when 'c' number of cameras are sold. The domain represents the number of cameras that are sold by the store.
So, negative profit means the store has a loss on selling that number cameras.
The store suffers loss upto 50 cameras sold. When the number of cameras sold is 50, there is neither loss not profit. At this point, total cost price equals total selling price. This is also break even point.
After this point, the store will have a net profit. So, for 62 cameras sold, the net profit of the store is $72.