Question

Water at a gauge pressure of 3.8 atm at street level flows into an office building at a speed of 0.62 m/s through a pipe 5.3 cm in diameter. The pipe tapers down to 3.0 cm in diameter by the top floor, 18 m above, where the faucet has been left open. Calculate the flow velocity and the gauge pressure in such a pipe on the top floor. Assume no branch pipes and ignore viscosity.

Answer 1

P₂ = 206945 Pa

Step-by-step explanation:

given,

gauge pressure = 3.8 atm

1 atm = 101325 Pa

speed of flow,v₁ = 0.62 m/s

diameter of pipe,d₁ = 5.3 cm

diameter of pipe after tapering, d₂ = 3 cm

height above the ground = 18 m

Using equation of continuity

A₁v₁ = A₂ v₂

`(\pi)/(4)d_1^2 v_1 = (\pi)/(4)d_2^2 v_2`

`v_2 = v_1((d_1^2)/(d_2^2))`

`v_2 =0.62* ((5.3^2)/(3^2))`

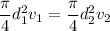
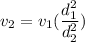
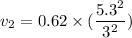
v₂ = 1.94 m/s

using Bernoulli's equation

`P_1 + (\rho v_1^2)/(2) = P_2 + (\rho v_2^2)/(2) +\rho g h`

`P_2= P_1 + (\rho)/(2)(v_1^2 - v_2^2) -\rho g h`

`P_2=3.8* 101325 + (1000)/(2)(0.62^2 - 1.94^2) -1000* 9.8* 18`

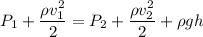
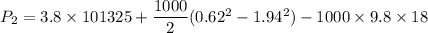
P₂ = 206945 Pa

hence, pressure of the pipe at top floor is equal to P₂ = 206945 Pa