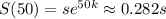If
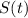 is the amount of strontium-90 present in the area in year
is the amount of strontium-90 present in the area in year
 , and it decays at a rate of 2.5% per year, then
, and it decays at a rate of 2.5% per year, then
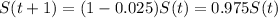
Let
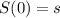 be the starting amount immediately after the nuclear reactor explodes. Then
be the starting amount immediately after the nuclear reactor explodes. Then
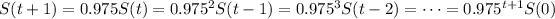
or simply
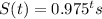
So that after 50 years, the amount of strontium-90 that remains is approximately
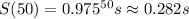
or about 28% of the original amount.
We can confirm this another way; recall the exponential decay formula,
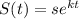
where
 is measured in years. We're told that 2.5% of the starting amount
is measured in years. We're told that 2.5% of the starting amount
 decays after 1 year, so that
decays after 1 year, so that

Then after 50 years, we have