Answer: First option.
Explanation:
Below are shown some transformations for a function
 :
:
1. If
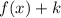 , the function is translated "k" units up.
, the function is translated "k" units up.
2. If
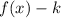 , the function is translated "k" units down.
, the function is translated "k" units down.
3. If
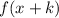 , the function is translated "k" units to the left.
, the function is translated "k" units to the left.
4. If
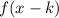 , the function is translated "k" units to the right.
, the function is translated "k" units to the right.
In this case, you can observe in the graph that the function
 intersects the y-axis at:
intersects the y-axis at:
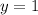
And the function
 intersects the y-axis at:
intersects the y-axis at:
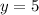
Knowing this, you can idenfity that:
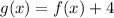
Therefore, you can conclude that the statement that best describes the translation of
 to
to
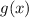 is: "Translation of four units up".
is: "Translation of four units up".