Question

Mason launched a model rocket from the group with an initial velocity of 160 feet per second. The path of the rocket can be modeled using the equation h=-16t^2 + 160t, where h is the height above ground and t is the time after launch. At what time(s) is the rocket at a height of 336 feet?

Answer 1

So, at time t = 3 s and t = 7 s ,Rocket will be at a height of 336 feet,

Explanation:

Given:

initial velocity of rocket = 160 feet/s

`h=-16t^(2)+160t`

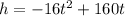
where ,h = height

t = time

To Find:

Time = ? for h =336 feet

Solution:

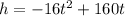`h=-16t^(2)+160t` ......Given

Substitute h = 336 we get

`336=-16t^(2)+160t\\16t^(2)-160t+336=0`

Now Dividing the Equation throughout by 16 we get

`t^(2)-10t+21=0`

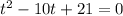
Which is a Quadratic Equation , hence on Factorizing we get

`t^(2)-7t-3t+21=0\\t(t-7)-3(t-7)=0\\(t-3)(t-7)=0\\t-3=0\ or\ t-7=0\\t=3\ or\ t=7`

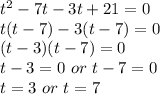
Because it is a Parabolic Path ,

So, during upward journey at t = 3 s, the height will reach 336 ft.

So, it will cross the same height at another time which is at t = 7 s

Again during downward journey, the height will be 336 from reference level at 7 s .

So, at time t = 3 s and t = 7 s ,Rocket will be at a height of 336 feet,