Question

Best Cup in Town sells two different types of coffee beans. The more expensive one (x) sells for $10 per pound, and the cheaper one (y) sells for $7 per pound. The shop also sells a 40 pound mixture of the two kinds of coffee beans for $9 per pound. Which system of linear equations can be used to determine how many pounds of each coffee is in the 40 pound mixture?

A) 10x + 7y = 360
x + y = 40

B) 10x + 7y = 40
x + y = 360

C) 10x + 7y = 360
x − y = 40

D) 7x + 10y = 360
x + y = 40

Answer 1

10x + 7y = 360

x + y = 40

x = $10 coffee beans; y = $7 coffee beans

total value → 10x + 7x = 9(40) → 10x + 7x = 360

total pounds → x + y = 40

Answer 2

Option A

The system of equations are x + y = 40 and 10x + 7y = 360

Solution:

Let pounds of expensive coffee beans be x

Let pounds of cheaper coffee bean be y

Cost of 1 pound of expensive coffee bean = $ 10

Cost of 1 pound of cheaper coffee bean = $ 7

The shop also sells a 40 pound mixture of the two kinds of coffee beans

pounds of expensive coffee beans + pounds of cheaper coffee bean = 40

x + y = 40 ------ eqn 1

The shop also sells a 40 pound mixture of the two kinds of coffee beans for $9 per pound

pounds of expensive coffee beans x Cost of 1 pound of expensive coffee bean + pounds of cheaper coffee bean x Cost of 1 pound of cheaper coffee bean = 40 pound mixture x $ 9

`x * 10 + y * 7 = 40 * 9`

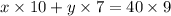
10x + 7y = 360 --------- eqn 2

Thus the system of equations are x + y = 40 and 10x + 7y = 360

Thus option A is correct