Question

Find the perimeter of the triangle with vertices ​A(negative 2​,2​,3​), ​B(4​,negative 4​,3​), and ​C(7​,6​,4​).

Answer 1

`P\approx 28.872\,\text{units}`

Explanation:

We are given coordinates of each of the vertices of the triangle ABC, hence we can use the distance formula to find the lengths of each of the side.

the distance formula is generally written as:

`r = √((x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2)`

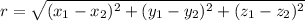
for the side AB: A(-2,2,3) and B(4,-4,3)

`AB = √((-2-4)^2+(2-(-4))^2+(3-3)^2)`

`AB = √((-6)^2+(6)^2+(3-3)^2)`

`AB = √(72)`

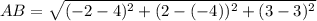
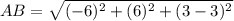
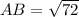
for the side BC: B(4,-4,3) and C(7,6,4)

`BC = √((4-7)^2+((-4)-6)^2+(3-4)^2)`

`BC = √(110)`

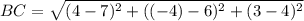
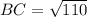
for the side CA: C(7,6,4) and A(-2,2,3)

`CA = √((7-(-2))^2+(6-2)^2+(4-3)^2)`

`CA = √(98)`

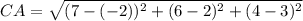
Now we all the sidelengths:

to find the perimeter we need to just sum the three side lengths:

`P = AB + BC + CA`

`P = √(72) + √(110) + √(98)`

`P\approx 28.872\,\text{units}`

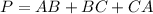
this is the perimeter of triangle ABC