Question

A 15 kg runaway grocery cart runs into a spring with spring constant 230 N/m and compresses it by 56 cm .What was the speed of the cart just before it hit the spring?

Answer 1

To solve this problem we will apply the concepts related to the conservation of kinetic energy and elastic potential energy. Thus we will have that the kinetic energy is

`KE = (1)/(2) mv^2`

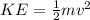
And the potential energy is

`PE = (1)/(2) kx^2`

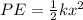
Here,

m = mass

v = Velocity

x = Displacement

k = Spring constant

There is equilibrium, then,

KE = PE

`(1)/(2) mv^2 = (1)/(2) kx^2`

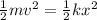
Our values are given as,

`x=0.56m\\k=230N/m\\m=15kg`

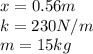
Replacing we have that

`(1)/(2) (15)v^2 = (1)/(2) (230)(0.56)^2`

`v = 2.19m/s`

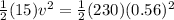
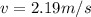
Therefore the speed of the cart is 2.19m/s