Question

Find the equation of the plane passing through the point (3, – 3, 1) and perpendicular to the line joining the points (3, 4, – 1) and (2, – 1, 5).

Answer 1

x+5y-6z+18 =0

Explanation:

We have to find the equation of the plane passing through the point (3, – 3, 1) and perpendicular to the line joining the points A(3, 4, – 1) and B(2, – 1, 5).

The perpendicular line joining AB is normal to the plane.

Direction ratios of AB are =
`(2-3, -1-4, 5-(-1))\\=(-1, -5, 6)`

this is direction ratios of normal

The plane passes through the point (3,-3,1)

Hence equation of the plane in normal form is

`-1(x-3) -5(y+3)+6(z-1) =0`

`-1x+3 -5y-15+6z-6 =0`

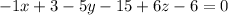
x+5y-6z+18 =0 is the equation of the plane.