Answer:
See explanation below.
Step-by-step explanation:
For this case we atart fom the proportional model given by the following differential equation:
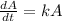
And if we rewrite this expression we got:
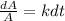
If we integrate both sides we got:
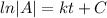
And using exponential on both sides we got:
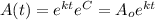
Where
 represent the initial amount for the isotope and t the time in years and A the amount remaining.
represent the initial amount for the isotope and t the time in years and A the amount remaining.
If we want to apply a model for the half life we know that after some time definfd
 the amount remaining is the hal, so if we apply this we got:
the amount remaining is the hal, so if we apply this we got:
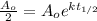
We can cancel
 and we got:
and we got:
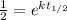
If we solve for k we can apply natural log on both sides and we got:
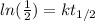
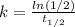
And that would be our proportional constant on this case.
If we replace this value for k int our model we will see that:
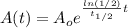
And using properties of logs we can rewrite this like that:
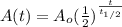
And thats the common formula used for the helf life time.