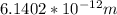To solve this problem we will start from the conservation of energy. Here we will have that the kinetic energy must be equivalent to the potential energy. That is
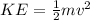
Here,
m = mass
v = Velocity
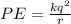
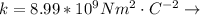 Coulomb constant
Coulomb constant
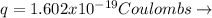 Charge Proton
Charge Proton
r = Distance
Equation both expression we have that
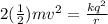
The kinetic energy is multiplied by two, by the existence of the two protons.
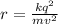
Replacing the values we have that
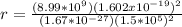
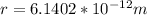
Therefore the distance of closest approach is