Answer:
a.
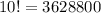 ;
;
b.
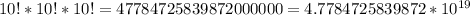
Explanation:
We need here to apply the Multiplication Principle or the Fundamental Principle of Counting for each answer. Answer b needs an extra reasoning for being completed.
The Multiplication Principle states that if there are n ways of doing something and m ways of doing another thing, then there are n x m ways of doing both (Rule of product (2020), in Wikipedia).
In how many ways can ten students line up?
There are ten students. When one is selected, there is no other way to select it again. So, no repetition is allowed.
Then, in the beginning, there are 10 possibilities for 10 students; when one is selected, there are nine possibilities left. When another is selected, eight possibilities are left to form the file, and so on.
Thus, we need to multiply the possibilities after each selection: that is why the Multiplication Principle is important here.
This could be expressed mathematically using n!:
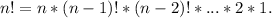
For instance,
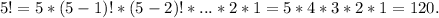
So, for the case in question, the ten students can line up in:
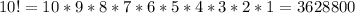 ways to line up in a single file.
ways to line up in a single file.
Second Question
For this question, we need to consider the former reasoning with extra consideration in mind.
The members of Group 1 can occupy only the following places in forming the file:
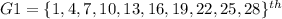 places.
places.
The members of Group 2 only:
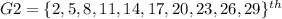 places.
places.
And the members of Group 3, the following only ones:
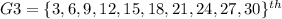 places.
places.
Well, having into account these possible places for each member of G1, G2 and G3, there are: 10! ways for lining up members of G1; 10! ways for lining up members of G2 and, also, 10! ways for lining up members of G3.
After using the Multiplication Principle, we have, thus:
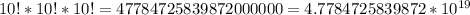 ways the students can line up to come in from recess.
ways the students can line up to come in from recess.