Question

The dot product can be used to determine the square of the magnitude of a vector v. Which of the following expressions represents the square of the magnitude of a​ vector?a. v/|v|b. v.|v|c. v.vd. v^2.v^2

Answer 1

vvv

Explanation:

Answer 2

c) v.v

Explanation:

The Dot product also known as scalar product or inner product is the multiplication of two equal length vectors which results in a scalar.

Mathematically,

`a.b=|a|*|b|*cos(\alpha)`

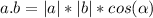
where
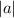`|a|` and
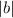`|b|` are the magnitudes of the vectors a and b

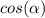`cos(\alpha)` is the angle between vectors a and b

If a and b are in the same direction then
`cos(\alpha)=1`

`a.b=|a|*|b|`

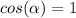
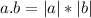
if a and b are orthogonal (90°) then
`cos(\alpha)=0`

`a.b=0`

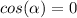
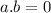
To represent the square of the magnitude of a vector v

`v.v=|v|*|v|=|v|^2`

Hence option c is the correct answer

a. v/|v|

Here vector v is divided by its own magnitude

b. v.|v|

Here vector v is multiplied by its own magnitude

c. v.v

Represents the square of the magnitude of vector v

d. v^2.v^2

Represents the dot product of square of vector v