Question

Suppose you wish to fabricate a uniform wire out of 1.10 g of copper. If the wire is to have a resistance R = 0.390 Ω, and if all the copper is to be used, What will be the length of the wire?

Answer 1

To solve this problem we will apply the concepts related to volume, as a function of length and area, as of mass and density. Later we will take the same concept of resistance and resistivity, equal to the length per unit area. Once obtained from the known constants it will be possible to obtain the area by matching the two equations:

Mass of copper wire
`(m) = 1.10g = 1.10*10^(-3) kg`

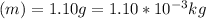
Density
`(\rho)= 8.92*10^3kg/m^3`

Resistively of copper
`(\gamma) = 1.7*10^(-8)\Omega \cdot m`

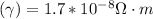
Resistance (R) = 0.390\Omega

Volume is defined as,

`V= lA \text{ and }(m)/(\rho)`

`lA= (1.10*10^(-3))/(8.92*10^3)`

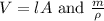
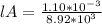
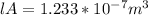`lA = 1.233*10^(-7) m^3` (1)

We know that,

`(l)/(A) = (R)/(\gamma)`

`(l)/(A)= (0.390\Omega)/(1.7*10^(-8)\Omega m)`

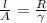
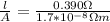
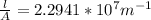`(l)/(A) = 2.2941*10^7 m^(-1)` (2)

Multiplying equation we have

`l^2 = (1.233*10^(-7))( 2.2941*10^7)`

`l^2 = 2.8286m^2`

`l =√(2.8286m^2)`

`l = 1.68m`

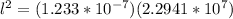
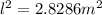
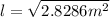
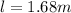
Therefore the length of the wire is 1.68m