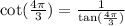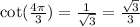Answer:
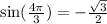
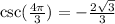
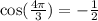
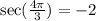
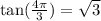
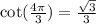
Explanation:
We are asked to find the exact trigonometric ratio for given angle
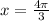 .
.
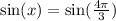
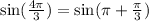
Using summation identity, we will get:
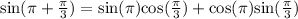
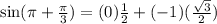
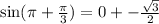
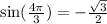
Let us find
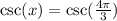
We will use identity

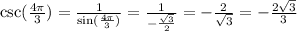
Now, we will solve for cos(x).
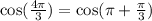
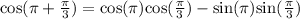
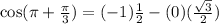
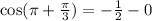
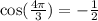
Let us find sec(x).
We will use identity
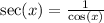
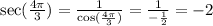
Let us find tan(x).
We will use identity
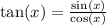 .
.
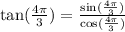
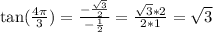
Let us find cot(x).
We will use identity
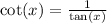 .
.