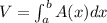Question

Use calculus to find the volume of the following solid S:

The base of S is a circular disk with radius r. Parallel cross- sections perpendicular to the base are squares.
Volume = ____________

Answer 1

`V=\int_(a)^(b)A(x)dx`

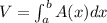
Explanation:

1) If we use Integration to find the volume of a solid S, making parallel cross sections perpendicular to its base and to the x-axis. Then we can make some assumptions.

2) Setting two points x=a, and x=b in the x axis and this solid is defined by a continuous function, made up by squares.

3) We can say that is possible to calculate the volume as the Summation of many slices, i.e. circular disks, of this solid just as the Riemman Sum for the areas.

4) Then we write this as:

`V\approx \sum_(i=1)^(n)A(x_(i))\Delta x`

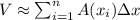
Ax=height Δx=width

This approximation gets better and better if we increase the number of circular disks:

`V=\lim_(n\rightarrow \infty )\sum_(i=1)^(n)A(x_(i))\Delta x`

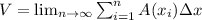
This is the same as to say:

`V=\int_(a)^(b)A(x)dx`