Question

find an equation of the line that passes through the point (1,-2) and is parallel to the line passing through the point (-2,-1) and (4,3)

Answer 1

2x - 3y = 8 is the equation of the line that passes through the point (1,-2) and is parallel to the line passing through the point (-2,-1) and (4,3)

Solution:

We have to find the equation of the line that passes through the point (1, -2) and is parallel to the line passing through the point (-2, -1) and (4, 3)

Let us first find the slope of line

We know slope of a line and slope of line parallel to it are equal

So we can find the slope of line passing thorugh the point (-2, -1) and (4, 3)

The slope of line is given as:

`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

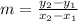
The points are (-2, -1) and (4, 3)

`(x_1, y_1) = (-2, -1)\\\\(x_2,y_2) = (4, 3)`

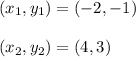
Substituting the values we get,

`m = (3-(-1))/(4-(-2))\\\\m = (4)/(6)\\\\m = (2)/(3)`

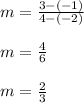
Thus the slope of line passing thorugh the point (-2, -1) and (4, 3) is
`m = (2)/(3)`

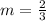
So the slope of line parallel to it also
`m = (2)/(3)`

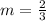
Now find the equation of the line that passes through the point (1, -2) with slope
`m = (2)/(3)`

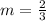
The equation of line in slope intercept form is given as:

y = mx + c ---- eqn 1

Where "m" is the slope of line and c is the y - intercept

Substitute (x, y) = (1, -2) and
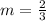`m = (2)/(3)` in eqn 1

`-2 = (2)/(3)(1) + c\\\\-2 = (2+3c)/(3)\\\\2 + 3c = -6\\\\3c = -8\\\\c = (-8)/(3)`

`\text{ Substitute } m = (2)/(3) \text{ and } c = (-8)/(3) \text{ in eqn 1 }`

`y = (2)/(3)x-(8)/(3)`

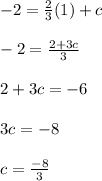
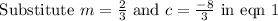
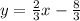
Writing in standard form, we get

`y = (2x-8)/(3)\\\\3y = 2x - 8\\\\2x -3y = 8`

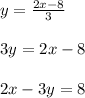
Thus the equation of line is found