Answer:

Explanation:
Given radius = 5 units, arc length of BA = π, arc length of CD = 3π
Circumference of a circle = 2πr
= 2π(5)
= 10π
To find the arc measure of BA:
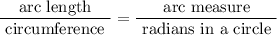
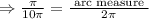
⇒ arc measure =
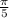
To find the arc measure of CD:
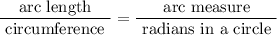
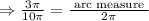
⇒ arc measure =
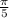 )
)
⇒ arc measure =
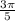
The measure of an inscribed angle is half of the measure of the arc it intercepts.
arc measure of BA =
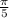 , then
, then
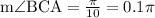
Similarly, arc measure of CD =
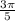 , then
, then
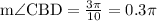
We know that sum of the interior angles of a triangle BCE = π
0.1π + 0.3π + m∠BEC = π
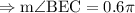
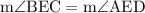 (by vertical angle theorem)
(by vertical angle theorem)
Hence, the measure of
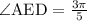 .
.