Question

Columbia manufactures bowling balls with a mean weight of 14.6 pounds and a standard deviation of 3 pounds. A bowling ball is too heavy to use and is discarded if it weighs over 16 pounds. Assume that the weights of bowling balls manufactured by Columbia are normally distributed. (Round probabilities to four decimals).What is the probability that a randomly selected bowling ball is discarded due to being too heavy to use?

Answer 1

0.3204 or 32.04%

Explanation:

Population mean weight (μ) = 14.6 pounds

Standard deviation (σ) =3 pounds

Assuming a normal distribution, for any given weight 'X' the correspondent z-score is determined by:

`z=(X-\mu)/(\sigma) \\`

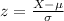
For X= 16 pounds:

`z=(16-14.6)/(3)\\z=0.4667`

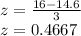
A z-score of 0.4667 is equivalent to the 67.96-th percentile of the distribution, the probability of a ball being discarded is:

`P(z>0.4667) = 1- 0.6796 = 0.3204`

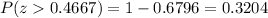
The probability that a randomly selected bowling ball is discarded due to being too heavy to use is 0.3204 or 32.04%