Question

A 500 kg car (mass of the car and riders) is at the top of a 28.5 m hill. Assuming no friction, what should the velocity of

the car be at the bottom of the hill? Show your work with units.

Answer 1

23.63 m/s

Step-by-step explanation:

We can assign the bottom of the hill to have zero potential energy.

Thus, the car has only potential energy at the top of the hill.

At the bottom of the hill, all of the potential energy is converted into kinetic energy.

Therefore, initial potential equals final kinetic:

`\displaystyle U_i = KE_f`

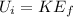
Substitute:

`\displaystyle mgh_i = (1)/(2)mv_f^2`

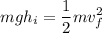
Solve for final velocity:

`\displaystyle v_f = √(2gh_i)`

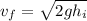
Therefore, the velocity of the car at the bottom of the hill is:

`\displaystyle \begin{aligned} v_f & = \sqrt{2(9.8\text{ m/s$^2$})(28.5\text{ m}) \\ \\ & = 23.63\text{ m/s} \end{aligned}`

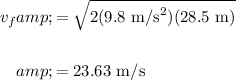
In conclusion, the velocity of the car at the bottom of the hill is about 23.63 m/s.