Question

List all possible rational roots. Then use synthetic division to confirm which rational roots exist:

2x ³+6x ²-1x-10=0

Answer 1

`\boxed{(1) \, x = \, \pm (1)/(2), \pm 1, \pm2, \pm (5)/(2), \pm 5, \pm 10; (2) \, x = -2}`

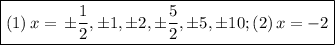
Explanation:

2x³+ 6x² - x - 10 = 0

(1) Possible roots

The Rational Roots Theorem states that, if a polynomial has any rational roots, they will have the form p/q, where p is a factor of the constant term and q is a factor of the leading coefficient.

`\text{Possible rational root} = ( p )/( q ) = \frac{\text{factor of constant term}}{\text{factor of leading coefficient}}`

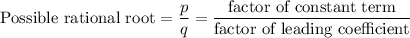
In your function, the constant term is -10 and the leading coefficient is 2, so

`\text{Possible root} = \frac{\text{factor of 10}}{\text{factor of 2}}`

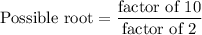
Factors of 10 = ±1, ±2, ±5, ±10

Factors of 2 = ±1, ±2

`\text{Possible roots are } \large \boxed{\mathbf{x = \pm (1)/(2), \pm 1, \pm2, \pm (5)/(2), \pm 5, \pm 10}}`

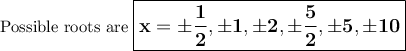
(2) Synthetic division

Rather than work through all 12 possibilities, I will do one that works.

`\begin{array}r-2 & 2 & 6 & -1 & -10\\& & -4& -4 & 10\\& 2 & 2& -5 & 0\\\end{array}`

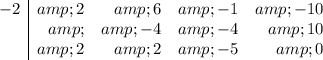
So, x = -2 is a root, and the quotient is 2x² + 2x - 5.

(3) Check for other rational roots

2x² + 2x - 5 = 0

D = b² - 4ac =2²- 4(2)(-5) = 4 + 40 = 44

√44 = 2√11, which is irrational.

Since irrational roots come in pairs, the cubic equation has two real, irrational roots and one rational root at x = -2.