Question

A compressed spring, with spring constant 1900 N/m, is sitting on a level, frozen lake. One end of the spring is anchored firmly at one end to a large rock that pokes through the ice, and the other touches a 3.5 kg, rectangular block of ice. The spring is compressed a distance of 15 cm. the ice is very smooth and is slightly wet, making it, for all practical purposes, frictionless. a) what is the potential energy of the spring when it is compressed? b) the spring is released, which then pushes the block across the ice. What is the kinetic energy of the ice block as it moved across the ice? c) what is the speed of the block of ice, once it is moving on the frozen lake? d) the block of ice now slides up an icy ramp (also smooth and slightly wet). What is the gravitational potential energy of the block when it reaches the highest point on the ramp? e) when the block is at its highest point on the ramp, how high above the frozen lake will it be?

Answer 1

21.375 J

21.375 J

3.49489 m/s

21.375 J

0.62254 m

Step-by-step explanation:

k = Spring constant = 1900 N/m

x = Displacement of spring = 15 cm

g = Acceleration due to gravity = 9.81 m/s²

m = Mass of block = 3.5 kg

Potential energy is given by

`U=(1)/(2)kx^2\\\Rightarrow U=(1)/(2)1900* 0.15^2\\\Rightarrow U=21.375\ J`

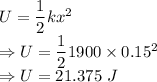
The potential energy of the spring is 21.375 J

As the energy in the system is conserved we get the kinetic and potential energy are equal

`(1)/(2)mv^2=21.375\\\Rightarrow v=\sqrt{(2* 21.375)/(3.5)}\\\Rightarrow v=3.49489\ m/s`

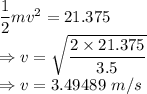
The velocity of block is 3.49489 m/s

Again, as the energy of the system is conserved

The gravitational potential energy is 21.375 J

`mgh=21.375\\\Rightarrow h=(21.375)/(3.5* 9.81)\\\Rightarrow h=0.62254\ m`

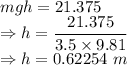
The height the block will reach is 0.62254 m