Answer:
Assuming that temperature and the rate law stayed unchanged, the concentration after
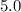 minutes would be
minutes would be
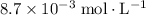 .
.
Step-by-step explanation:
The rate law is a function that takes the concentrations of the reactants as its input and return the rate of the reaction at that given time. In this case, since there's only one reactant, the rate law would be in the form:
![\text{Rate} = k \cdot [{\rm CH_3CHO\; (g)}]^(n)](https://img.qammunity.org/2021/formulas/chemistry/middle-school/hddwf9n2gamvq3xmnqw14oj6m2zq6ozju4.png) ,
,
where
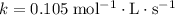 is the rate constant, and
is the rate constant, and
 is the order of the reactant
is the order of the reactant
![[{\rm CH_3CHO\; (g)}]](https://img.qammunity.org/2021/formulas/chemistry/middle-school/y6gldk9cq0aba17h6ra4qhi3q6ghshysvi.png) in this reaction.
in this reaction.
The question stated that this reaction is of second order. In other words, the order of this reaction is
 . By definition, the order of a reaction is the sum of the orders of all the reactants in the rate law. In this case, since
. By definition, the order of a reaction is the sum of the orders of all the reactants in the rate law. In this case, since
![[\rm CH_3CHO\; (g)]](https://img.qammunity.org/2021/formulas/chemistry/middle-school/420qrn5j9kxnjgzjbwwiidalakiljean70.png) is the only reactant, its should must also be
is the only reactant, its should must also be
 . That is:
. That is:
 and
and
![\text{Rate} = k \cdot [{\rm CH_3CHO\; (g)}]^2](https://img.qammunity.org/2021/formulas/chemistry/middle-school/2srshrjqxt4s8j3sk2ck28ob3t9bqbwxnu.png) .
.
This rate law can be solved as a differential equation. To keep the expressions simple, let
 (with the unit
(with the unit
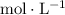 ) represent the concentration of
) represent the concentration of
![[\rm CH_3CHO\; (g)]](https://img.qammunity.org/2021/formulas/chemistry/middle-school/420qrn5j9kxnjgzjbwwiidalakiljean70.png) . That is: let
. That is: let
![x = [\rm CH_3CHO\; (g)]](https://img.qammunity.org/2021/formulas/chemistry/middle-school/cjbgx492ndrnuejim4gal207m4x9gfpbxa.png) .
.
The reaction rate of a chemical reaction is the opposite of first derivative of concentration with respect to time
 (in seconds.) (There should be a negative sign, since the concentration of the reactants was supposed to decrease.) In this case,
(in seconds.) (There should be a negative sign, since the concentration of the reactants was supposed to decrease.) In this case,
![\displaystyle \text{Rate} = -(d)/(dt)\, \left([\rm CH_3CHO\; (g)]\right) = -(dx)/(dt)](https://img.qammunity.org/2021/formulas/chemistry/middle-school/91vd50zal7m2vp12cbg6xyhsu2fauz6ksu.png) .
.
That would be the left-hand side of the rate law. The right-hand side would become:
![k\cdot [{\rm CH_3CHO\; (g)}]^2 = k \, x^2](https://img.qammunity.org/2021/formulas/chemistry/middle-school/aeub56744g97jenud6495u8xhpdqi83sju.png) .
.
Equate the two halves to obtain the differential equation:
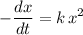 .
.
Group the two variables with their respective differentials. That is: rewrite the equation such that
 is on the same side as
is on the same side as
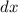 while
while
 is on the same side as
is on the same side as
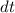 . Note that in this case there's no such variable as
. Note that in this case there's no such variable as
 . Simply leave
. Simply leave
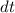 alone on one side of the equation and all the
alone on one side of the equation and all the
 and
and
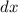 on the other side.
on the other side.
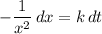 .
.
Integrate both sides (indefinitely, i.e., without knowing what the bounds are:)
![\displaystyle \int\left[-(1)/(x^2)\, dx\right] = \int\left[k\, dt\right]](https://img.qammunity.org/2021/formulas/chemistry/middle-school/q1pwae1s14wbbv0002ezshb1kn6dnr35sd.png) .
.
For the left-hand side, apply the power rule for integration. For the right-hand side, keep in mind that
 is simply a constant and is not dependent on the value of
is simply a constant and is not dependent on the value of
 . Since this integration is indefinite, add a constant of integration
. Since this integration is indefinite, add a constant of integration
 to one side of the equation.
to one side of the equation.
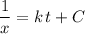 .
.
Rearrange the equation to obtain an expression of concentration
 at time
at time
 :
:
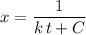 .
.
Substitute in the value for
 :
:
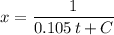 .
.
At time
 (initial condition,) the concentration is
(initial condition,) the concentration is
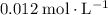 . Hence, the constant
. Hence, the constant
 here should ensure that when
here should ensure that when
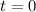 ,
,
 . Solve the equation for
. Solve the equation for
 :
:
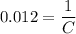 .
.
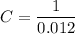 .
.
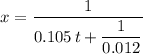 .
.
Evaluate this expression at
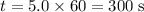 .
.
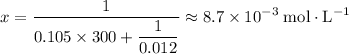 .
.
That's the concentration five minutes after the initial condition.