Question

A child's water pistol shoots water through a 1.0-mm-diameter hole. If the pistol is fired horizontally 70 cm above the ground, a squirt hits the ground 1.2 m away.What is the volume flow rate during the squirt? Ignore air resistance.( In mL/s).

Answer 1

2.52 ml/s

Step-by-step explanation:

Unit conversions:

1 mm = 0.001m

70 cm = 0.7 m

Let g = 10m/s2. If the pistol is fired horizontally at first, it did not have an vertical velocity, only horizontal velocity. So g is the only thing that affects the vertical motion of water.

We can calculate the time it takes for the squirts to hit the ground in the following equation of motion:

`h = gt^2/2`

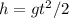
where h = 0.7 m is the vertical distance, and t is the time it takes, which is what we are solving for:

`t^2 = 2h/g = 2*0.7/10 = 0.14`

`t = √(0.14) = 0.374 s`

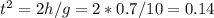
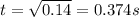
So the squirts takes 0.374s to hit the ground, and within that time it travels a distance of 1.m horizontally. Neglect air resistance, we can calculate the horizontal velocity:

`v = s/t`

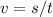
where s = 1.2 m is the horizontal distance

`v = 1.2/0.374 = 3.21 m/s`

The cross-section area of the hole is

`A = \pi r^2`

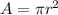
where r = d/2 = 0.001/2 = 0.0005 m is the radius of the hole

`A = 0.0005^2 \pi = 7.85*10^(-7)`

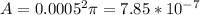
So we can calculate the volume flow rate:

`\dot{V} = v*A = 3.21*7.85*10^(-7) = 2.52 * 10^(-06) m^3/s`

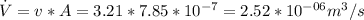
or 2.52 ml/s