Question

An LP turntable must spin at 3.500 rad/s to play a record. How much torque must the motor deliver if the turntable is to reach its final angular speed in 1.800 revolutions, starting from rest? The turntable is a uniform disk of diameter 30.80 cm and mass 0.2500 kg.

Answer 1

0.00321 Nm

Step-by-step explanation:

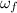`\omega_f` = Final angular velocity = 3.5 rad/s

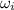`\omega_i` = Initial angular velocity = 0

`\alpha` = Angular acceleration

`\theta` = Angle of rotation = 2 rev

Equation of rotational motion

`\omega_f^2-\omega_i^2=2\alpha \theta\\\Rightarrow \alpha=(\omega_f^2-\omega_i^2)/(2\theta)\\\Rightarrow \alpha=(3.5^2-0^2)/(2* 2\pi * 1.8)\\\Rightarrow \alpha=0.54156\ rad/s^2`

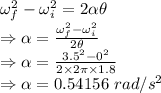
Moment of inertia is given by

`I=mr^2\\\Rightarrow I=0.25* 0.154^2\\\Rightarrow I=0.005929\ kgm^2`

Torque is given by

`\tau=I\alpha\\\Rightarrow \tau=0.005929* 0.54156\\\Rightarrow \tau=0.00321\ Nm`

The torque required is 0.00321 Nm