Answer:
The time for which motorist stop for gas and sandwich is 15 minutes
Explanation:
Given as :
Let The distance cover by motorist = d miles
Let The time for which motorist stop = n minutes
The time taken by motorist to cover d distance with no stop = t = 3 hours
The average speed of motorist with no stop = s = 65 miles per hour
Again
The time taken by motorist to cover d distance with stop = T hours
The average speed of motorist with stop = S = 60 miles per hour
∵ Distance = Speed × Time
So, with no stop
d = s × t
Or, d = 65 miles per hour × 3 hours
Or, d = 195 miles
And, with stop
d = S × T
Or, d = 60 miles per hour × T hours
∵ d = 195 miles
So, 60 miles per hour × T hours = 195 miles
Or , 60 T = 195
∴ T =
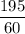
i.e T = 3.25 hours
Or, T = 3 hours +
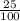 hours
hours
Or, T = 3 hours +
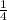 hours
hours
Or, T = 3 hours +
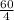 minutes
minutes
Or, T = 3 hours + 15 minutes
So, time taken by motorist to cover d distance with stop = T = 3 h + 15 min
Now,
The time for which motorist stop = time taken by motorist to cover d distance with stop - time taken by motorist to cover d distance with no stop
i.e n = T - t
Or, n = ( 3 hours + 15 minutes) - ( 3 hours)
∴ n = 15 minutes
So, The time for which motorist stop = n = 15 minutes
Hence, The time for which motorist stop for gas and sandwich is 15 minutes . Answer