Question

I) A circular coil with radius 20 cm is placed with it's plane parallel and between two straight

wires P and Q. The coil carries current I = 0.5A . I for coil is in clockwise direction when viewed
from left side. Wire P is located 40 cm to the left of a circular coil and carries current I = 0.2A
while wire Q is located 80 cm to the right of the circular coil and carries current l = 0.6A. Both
I for P and l for Q are in the same directions into the paper. Determine the resultant of magnetic field at
the centre of a circular coil from the top view.
ii) If the current in wire P is out of the page, determine the resultant of magnetic field at the centre
of a circular coil.
​

Answer 1

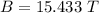`B=15.433\ T` inwards when viewing from the left side.

Step-by-step explanation:

Given:

• radius of the circular loop,
  `r=0.2\ m`

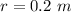
• current in the coil,
  `I_c=0.5\ A`

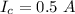
• Direction of current is clockwise when viewed from left.

• Distance of wire P from the loop,
  `d_p=0.4\ m`

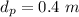
• Distance of wire Q from the loop,
  `d_q=0.8\ m`

• current in each wires P & Q,
  `I=0.2\ A`

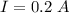
Now the magnetic field in coil will be inwards when viewed from left by the Maxwell's right hand thumb rule.

Magnitude is given by:

`B_c=(\mu_0.I_c)/(2R)`

`B_c=(4\pi* 10^(-7)* (0.5))/(2* 0.2)`

`B_c=15.7* 10^(-7)\ T`

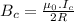
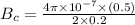
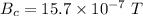
Now the effect of magnetic field due to wire P at the center of the loop:

(We get the effective distance as 0.4+0.2=0.6 m)

`B_P=(\mu_0.I)/(2\pi.d_p)`

`B_P=(4\pi* 10^(-7)* (0.2))/(2\pi* 0.6)`

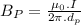
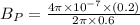
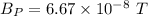`B_P=6.67* 10^(-8)\ T` coming out of the loop when viewed from left.

Now the effect of magnetic field due to wire Q at the center of the loop:

(We get the effective distance as 0.8+0.2=1 m)

`B_P=(\mu_0.I)/(2\pi.d_q)`

`B_P=(4\pi* 10^(-7)* (0.2))/(2\pi* 1)`

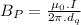
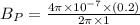
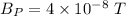`B_P=4* 10^(-8)\ T` going in to the loop when viewed from left.

Now the net resultant effect all the magnetic fields:

`B=B_c-B_P+B_Q`

`B=15.7-0.667+0.4`

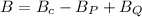
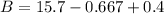
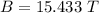`B=15.433\ T` inwards when viewing from the left side.