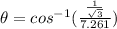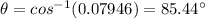Answer:
(a)
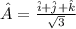
(b)
Solution:
As per the question:
Side of the cube, a = 4.4 cm
Coordinates of the diagonally opposite corner, A = <4.4, 4.4, 4.4> cm
Now,
(a) To calculate the unit vector:
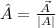
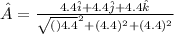
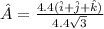
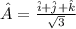
(b) To calculate the angle between the two vectors say A and A' is given by:
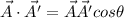
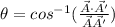 (1)
(1)
Now,
The coordinates of the diagonally opposite corner, A' is <0, 0, 1> cm
Thus
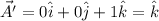
Now,
Using equation (1) :
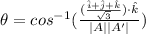
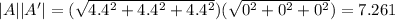
Thus