Answer:
The displacement of the elephant before it comes to a stop is 3301.8 m.
Step-by-step explanation:
Given:
Mass of elephant is,
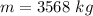
Initial velocity of elephant is,
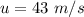
Final velocity of elephant is,

Stopping force exerted by the brakes is,

As per Newton's second law, net force is equal to the product of mass and acceleration.
So, the stopping force is equal to the product of mass of elephant and stopping acceleration. Therefore,
Stopping force (f) = mass (m) × stopping acceleration

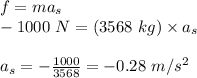
Now, using equation of motion, we find the total displacement of the elephant before it comes to a stop.
Let the total displacement be 'S'.
Using the equation of motion as below:
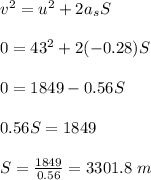
Therefore, the displacement of the elephant before it comes to a stop is 3301.8 m.