Question

According to Chebyshev's theorem, what percent of the values will fall between 100 and 124 for a data set that has a mean of 112 and a standard deviation of 4?

Answer 1

More than 88.889% of the values will fall between 100 and 124 for the data set that has a mean of 112 and a standard deviation of 4.

Explanation:

The Chebyshev's theorem states that the probability of any random variable ''X'' assuming a value between a range of ''k times'' the standard deviation is at least
`1-(1)/(k^(2))`

We can write mathematically this as :

P( μ - kσ < X < μ + kσ)
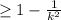`\geq 1-(1)/(k^(2))` (I)

Where μ is the mean and σ is the standard deviation.

In this exercise :

μ = 112

σ = 4

If we replace this values in the equation (I) :

`P(112-k(4)<X<112+k(4))\geq 1-(1)/(k^(2))`

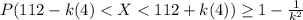
The percent of the values falling between 100 and 124 can be written as :

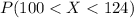`P(100<X<124)` (II)

This probability must be equal to
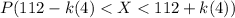`P(112-k(4)<X<112+k(4))` (III)

Therefore if we work with (II) and (III) ⇒

(II) = (III) ⇒

`P(100<X<124)=P(112-k(4)<X<112+k(4))` ⇒

`100=112-4k`

`124=112+4k`

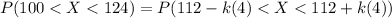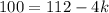
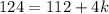
⇒ In any of the equations we find that

`12=4k`

`k=3`

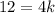
Finally, we can write that

`P(112-3(4)<X<112+3(4))=P(100<X<124)\geq 1-(1)/(k^(2))=1-(1)/(3^(2))=1-(1)/(9)`

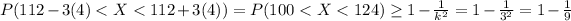
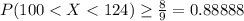`P(100<X<124)\geq (8)/(9)=0.88888` ≅ 88.889%

According to Chebyshev's theorem, more than 88.889% of the values will fall between 100 and 124 for the data set.