Question

What substitution should be used to rewrite 4x^4 -21x^2+20=0 as a quadratic equation

Answer 1

To rewrite the equation
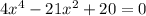`4x^4 - 21x^2 + 20 = 0` as a quadratic equation, we can substitute
`x^2` with a new variable y and solve for y using factoring or the quadratic formula. Finally, we substitute back and solve for x.

Step-by-step explanation:

To rewrite the equation
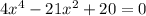`4x^4 - 21x^2 + 20 = 0`as a quadratic equation, we can make a substitution by introducing a new variable. Let's substitute
`x^2` with a new variable, let's say y. So our equation becomes
`4y^2 - 21y + 20 = 0`.

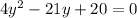Now this equation is in quadratic form. We can solve this equation by factoring or using the quadratic formula. Factoring, we find (2y - 5)(2y - 4) = 0. Setting each factor equal to zero gives us y = 5/2 and y = 4/2.

Since we substituted x^2 with y, we can now substitute back and solve for x. Taking the square root of y, we get x = ±√(5/2) and x = ±√(4/2).

Answer 2

u = x²

Step-by-step explanation:

4x⁴ − 21x² + 20 = 0

4(x²)² − 21x² + 20 = 0

If we substitute u = x²:

4u² − 21u + 20 = 0