Answer:
 64.5 %
64.5 %
Explanation:
Let's start defining the random variable X.
X : '' SAT critical reading scores from the 2014 school year for high school students in the United States ''
We know that X ~ N (μ,σ)
Where μ is the mean and σ is the standard deviation.
⇒ X ~ N (497,115)
If we want to calculate probabilities related to X we need to standardized the random variable. We do this by subtracting the mean to X and then dividing by the standard deviation. This new random variable will be ''Z'' and Z ~ N (0,1)
We can find the probabilies of ''Z'' in any standard normal table.
The cumulative distribution of ''Z'' is the function Φ where :
 Φ(a)
Φ(a)
Now, we need to calculate the following probability :

If we standardized this :

We know that
 ≅ Z ⇒
≅ Z ⇒
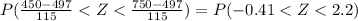 ⇒
⇒
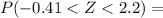 Φ(2.2) - Φ(-0.41) =
Φ(2.2) - Φ(-0.41) =
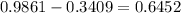
⇒ 64.52% ≅ 64.5%
We find that the probability (given as a percentage) is 64.5%