Question

Solve the following problems: △ABC ∼ △A1B1C1. Find angle measures x, y, z, w

Answer 1

Therefore angle measure are

`x=50\°\\y=70\°\\z=60\°\\w=70\°`

Explanation:

Given:

△ABC ∼ △A1B1C1.

∠A = 60°

∠B1 = 50°

∠B =x , ∠C = y , ∠A1 = z , ∠C1 = w

To Find:

angle measures,

x = ?, y = ? ,z = ?, w = ?

Solution:

△ABC ∼ △A1B1C1. .............Given:

If two triangles are similar then the corresponding angles of similar triangles are congruent.

∴ ∠A ≅ ∠A1 .............1

∠B ≅ ∠B1 .............2

∠C ≅ ∠C1 .............3

But ,∠A = 60° ,∠B1 = 50° given

∴ ∠A ≅ ∠A1 = 60° ................Transitive Property

∠B ≅ ∠B1 = 50° ................Transitive Property

Therefore

∠B =x = 50°, ∠A1 = z = 60° ,

Now,

In a Triangle sum of the measures of all the angles of a triangle is 180°.

In ΔABC we have

`\angle A+\angle B+\angle C=180`

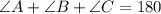
Substituting the given value we get

`60+50+y=180\\y=180-110=70\\y=70\°`

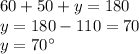
m∠C = y = 70°

But ∠C ≅ ∠C1 ............From 3

∴ ∠C1 = w = 70° ................Transitive Property

Therefore angle measure are

`x=50\°\\y=70\°\\z=60\°\\w=70\°`