Question

URGENT!! FIRST CORRECT ANSWER GETS 15 POINTS!!!

A function f is defined by f(x)= 3/17x+2. If x increases by 51, by how much does f(x) increase?

Answer 1

if x increases by 51, f (x) increases by 9.

Explanation:

Given function:

`f(x)=(3)/(17) x+2`

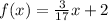
The above equation would have a constant slope as it seems to be a linear function. ‘x’, the coefficient of the variable x is the slope of the function. Here,

`x=(3)/(17)`

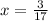
The rate of change of the function with respect to x referred as the slope of the function. Thus,

`slope =\frac{\text { change of } f(x)}{\text { change of } x}`

`(\Delta f)/(\Delta x)=(3)/(17)`

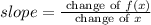
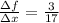
Given, x increases by 51. So, we have

`\Delta x=51`

`(\Delta f)/(51)=(3)/(17)`

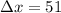
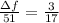
Now solve for ΔF,

`\Delta f=(3)/(17) * 51=3 * 3=9`

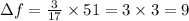
Thus, we have obtained that if x increases by 51, f (x) increases by 9.