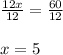Answer:
1. Distributive property.
2. Combining like terms.
3. Addition property of equality.
4. Division property of equality.
Explanation:
- The Distributive property states that:

- The Addition property of equality states that:
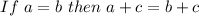
- The Subtraction property of equality states that:

- The Multiplication property of equality states that:
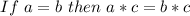
- The Division property of equality states that:

Given the following equation:
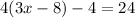
We can identify that the methods Maria used to solve it and the order, are:
1. Distributive property:
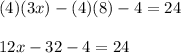
2. Combining (or adding) like terms:
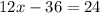
3. Addition property of equality, because she added 36 to both sides of the equation:

4. Division property of equality, because she divided both sides of the equation by 12: