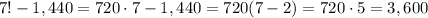Answer:
3,600
Explanation:
There are 5 green, 1 red, and 1 blue book on the shelf, 7 books in total.
First, count the number of ways when the red and the blue books are not separated. If these books are not separated, you can count them as one book, so there are 6 books in total which can be arranged in
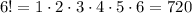
different ways.
But red and blue books can be rearranged in two ways: blue, red or red, blue, so the number of ways books can be arranged if the red and blue book are not separated is
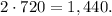
Hence, the number of ways books can be arranged if the red and blue book are separated is