Question

At a certain factory, the total cost of manufacturing q units during the daily production run is C(q)=q2+q+600 dollars. On a typical workday, q(t)=20t units are manufactured during the first t hours of a production run. (a) Express the total manufacturing cost as a function of t. (b) How much will have been spent on production by the end of the second hour? (c) When will the total manufacturing cost reach $7000?

Answer 1

a) C(t) = 400t² + 20t + 600

b) $2,240

c) 4 hours

Explanation:

Data provided in the question:

C(q) = q² + q + 600 ......................(1)

q(t) = 20t ..................(2)

Now,

a) total manufacturing cost as a function of t

substituting 2 in 1 we get

C(t) = (20t)² + (20t) + 600

or

C(t) = 400t² + 20t + 600 ..........(3)

b) at the end of 2 hour t = 2

therefore,

substituting t = 2 in equation 3

we get

C(2) = 400(2)² + 20(2) + 600

or

C(2) = 1600 + 40 + 600

or

C(2) = 2,240

c) For C(t) = $7,000

using equation (3)

we have

$7,000 = 400t² + 20t + 600

or

400t² + 20t = $6,400

or

20(20t² + t ) = $6,400

or

20t² + t = 320

or

20t² + t - 320 = 0 ............(4)

now finding the roots i.e value of 't'

`t = (-1\pm√(b^2-4ac))/(2a)`

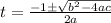
on comparing with the equation (4), we have

a = 20

b = 1

c = -320

therefore,

`t = (-1\pm√(1b^2-4(20)(-320)))/(2(20))`

or

⇒
`t =(-1\pm 160.003)/(40)`

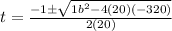
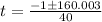
or

⇒ t = 3.97 and t = - 4.02

since time cannot be negative

therefore

t = 3.97 hours ≈ 4 hours