To solve this problem we will apply the relationship between Newton's second law and Hooke's law, with which we will define the balance of the system. From the only unknown in that equation that will be the constant of the spring, we will proceed to find the period of vibration of the car.
We know from Hooke's law that the force in a spring is defined as
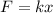
Here k is the spring constant and x the displacement
While by Newton's second law we have that the Weight can be defined as
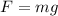
Here m is the mass and g the gravity acceleration.
The total weight would be
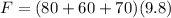
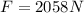
Each spring takes a quarter of the weight, then
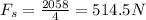
Since the system is in equilibrium the force produced by the weight in each spring must be equivalent to the force of the spring, that is to say
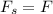
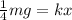
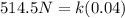
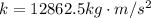
The period of a spring-mass system is given as
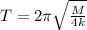
The total mass is equivalent as the sum of all the weights, then replacing we have that the Period is
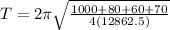
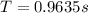
Therefore the period of vibration of the car as it comes to rest after the four get in is 0.9635s