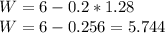Question

A grocery store produce manager is told by a wholesaler that the apples in a large shipment have a mean weight of 6 ounces and a standard deviation of 1.4 ounces. The manager is going to randomly select 49 apples. Suppose the manager is willing to risk a 10% chance of returning the shipment even if the wholesaler's claim is true. Let W be the mean weight of the sample below which the shipment will be returned. Find the value of W.

Answer 1

W= 5.744

Explanation:

given that a grocery store produce manager is told by a wholesaler that the apples in a large shipment have a mean weight of 6 ounces and a standard deviation of 1.4 ounces

Sample size n= 49

Margin of error = 0.10 (10% risk )

Let us assume X no of apples having mean weight of 6 oz is N(6,1.4)

Then sample mean will be normal with (6, 1.4/7) = (6,0.2)

(Because sample mean follows normal with std error as std dev /sqrt of sample size)

Now required probability <0.10

i.e.
`P(\bar X <W) <0.10`

Since x bar is normal we find z score for

`P(Z<z) < 0.10\\`

From std normal distribution table we find that z = 1.28

Corresponding X score =

`W= 6-0.2*1.28\\W= 6-0.256 = 5.744`