Value of x is:
Explanation:
Given Fraction,
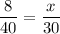
Further we can solve by cross multiplication,
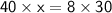
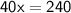
Divide both sides by 40,
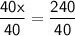
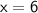
Verifying our answer.
Simply put the value of x in the given fraction ,

We know that,
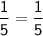
Hence, x = 6 makes a true equivalent fraction statement.