Question

Identifying Information Necessary for Applying the SSS

Similarity Theorem

Given that

what additional information is

POR using the SSS

needed to prove A DEF

similarity theorem?

DE 2 PO

6) Intro

Answer 1

The value of the proportion between:

`\frac{\overline{OR}}{\overline{EF}}=\frac{\overline{RP}}{\overline{FD}}`

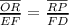
Explanation:

1) According to the criteria of Similarity of two Triangles, they both must share the same proportion on their corresponding sides. Imagining we have two triangles DEF and POR. They must follow this rule:

`\frac{\overline{PO}}{\overline{DE}}=\frac{\overline{OR}}{\overline{EF}}=\frac{\overline{RP}}{\overline{FD}}=k`

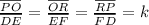
2) The question states that DE=2PO therefore the ratio between PO over DE is
`(1)/(2)`

Therefore we can say that

`\frac{\overline{PO}}{\overline{DE}}=(1)/(2)`

However nothing has been informed about the other legs of these two triangles.

3) Unless, the value of

`\frac{\overline{PO}}{\overline{DE}}=\frac{\overline{OR}}{\overline{EF}}=\frac{\overline{RP}}{\overline{FD}}=(1)/(2)`

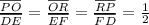
Anything can be said about the SSS theorem, for these two angles.