Question

Two children, Ferdinand and Isabella, are playing with a waterhose on a sunny summer day. Isabella is holding the hose in herhand 1.0 meters above the ground and is trying to spray Ferdinand,who is standing 10.0 meters away. I know so far that she cannotspray Ferdinand at the current position and with the curreentspeed of spray. I got stuck inthe following question:

To increase the range of the water, Isabellaplaces her thumb on the hose hole and partially covers it. Assumingthat the flow remains steady, what fraction Image for Two children, Ferdinand and Isabella, are playing with a waterhose on a sunny summer day. Isabella is holding of the cross-sectional area of the hose hole does shehave to cover to be able to spray her friend?

Assume that the cross section of the hoseopening is circular with a radius of 1.5 centimeters.

Answer 1

84.196%

Step-by-step explanation:

g = Acceleration due to gravity = 9.81 m/s²

`y_0=1\ m`

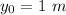
x = 10 m

t = Time taken

`v_0` = 3.5 m/s (assumed, as it is not given)

`A_0` =
`\pi 1.5^2`

We have the equation

`y=y_0+ut+(1)/(2)gt^2\\\Rightarrow 0=y_0-(1)/(2)gt^2\\\Rightarrow t=\sqrt{(2y_0)/(g)}\\\Rightarrow t=\sqrt{(2* 1)/(9.81)}\\\Rightarrow t=0.45152\ s`

`x=x_0+vt\\\Rightarrow 10=0+v0.45152\\\Rightarrow v=(10)/(0.45152)\\\Rightarrow v=22.14741\ m/s`

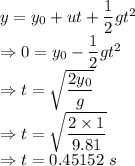
From continuity equation we have

`Av=A_0v_0\\\Rightarrow A=(A_0v_0)/(v)\\\Rightarrow A=(\pi 1.5^2* 3.5)/(22.14741)\\\Rightarrow A=1.11706\ cm^2`

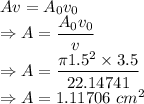
Fraction is given by

`f=(A_0-A)/(A_0)* 100\\\Rightarrow f=(\pi 1.5^2-1.11706)/(\pi 1.5^2)* 100\\\Rightarrow f=84.196\ \%`

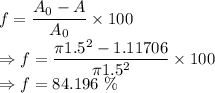
The fraction is 84.196%