Answer:
y = -3
Explanation:
METHOD 1:
The sloope-intercept form of an equation of a line:

m - slope
b - y-intercept
The formula of a sloe:
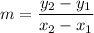
(x₁, y₁), (x₂, y₂) - points on a line
We have the points (-2, -3) and (1, -3).
Substitute:
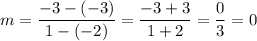
Put the value of the slope and the coordinates of the point (1, -3) to the equation of a line:

Finally:
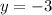
METHOD 2:
We can see that the second coordinates of the points (ordinate) are the same.
Conclusion: This is a horizontal line.
The equation of a horizontal line:
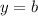
We have (-2, -3), (1, -3) → y = -3