Question

Find the equation of the line that contains the point (6, -2) and is perpendicular to the line y.

Answer 1

Equation of the perpendicular line will be
`y=(1)/(2)x-5`.

Explanation:

Given question is incomplete ; here is the complete question.

Find the equation of the line that contains the point (6,-2) and is perpendicular to the line y=-2⁢x+8.

Slope of the given line is (-2).

If the slope of the required line is m then,

m × (-2) = (-1) [Slopes of the perpendicular lines when multiplied equals to (-1)]

m =
`(1)/(2)`

Now the equation of the line passing through a point (6, -2) with slope
`(1)/(2)` will be

y - y' = m(x - x')

y + 2 =
`(1)/(2)(x-6)`

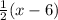
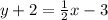
`y+2=(1)/(2)x-3`

y =
`(1)/(2)x-5`

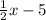
Therefore, equation of the perpendicular line will be
`y=(1)/(2)x-5`