Answer:
D.
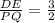
Explanation:
Given:
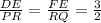
SSS Similarity theorem: Triangles are similar if all three sides in one triangle are in the same proportion to the corresponding sides in the other.
Applying SSS theorem to ΔDEF and Δ PQR :
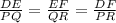
But
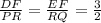
Therefore,
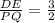
This is the additional information needed to show the triangles are similar as per SSS similarity theorem.